Magnetic Simulation

Finite-element model of a HDD write head above a granular media track.
Since the rise of high performance computing, numerical simulations are an integral part of material science. For magnetic materials the micromagnetic model has proven to be an excellent tool for the description of static properties of well as the dynamics of the magnetization on the nanoscale. The micromagnetic model is a semiclassical continuum model that accounts for classical fields as well as quantumechanical contributions like exchange coupling and that is able to resolve the inner structure of domain walls. The model is defined in terms of partial differential equations whose analytical solution is only possible for simple edge cases.
We use different discrete methods, namely the finite-element method (FEM) and the finite-difference method (FDM) to solve the micromagnetic equations numerically. We develop and implement optimized algorithms for CPU and GPU computing and apply them to a variety of problems. Our algorithmic research interests include fast time integration of stiff differential equations, solution of open boundary problems with the boundary-element method (BEM) and the fast-multipole method (FMM), coarse graining, energy-barrier calculation, and inverse magnetostatic problems.
We use our own simulation software to investigate the magnetic properties of sensors, hard disks, novel storage technologies like STT MRAM and racetrack memories. Each of these application areas has its own challenges. In the case of magnetic sensors, the main challenge is the system size. Typical sensors have sizes of multiple microns. In order to get accurate numerical results for the micromagnetic simulations, a discretization with millions of degrees of freedom is required. We use finite-difference micromagnetics with direct energy minimization in order to compute the hyteresis properties of these systems.
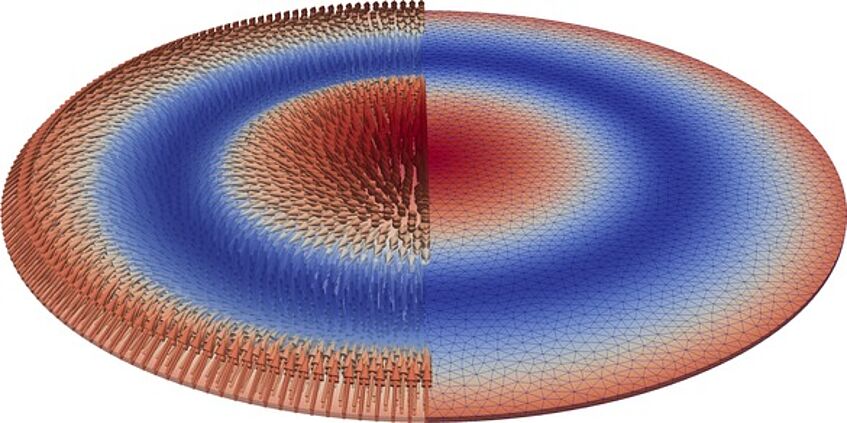
Skyrmion structure in a thin magnetic disk.
While the working principle of conventional hard-disk drives is well understood, new technologies are required to further increase the storage density of these devices that form the backbone of the recent big-data hype. A promising candidate to achieve this is heat-assisted magnetic recording (HAMR). We investigate the influence of temperature on the magnetization dynamics by means of atomistic simulations and use our own coarse graining strategies in the order to guide the design of HAMR devices.
With our finite-element software magnum.fe we are able to solve the micromagnetic equations coupled to a three-dimensional spin-diffusion model in a self consistent fashion. This allows us to simulate a variety of spintronics effects such as GMR, spin-transfer torque (STT) in multilayers as well as racetrack devices, spin-orbit torque (SOT), and (inverse) spin Hall effects. Besides the accurate description of MRAM and racetrack devices, this model can be used to investigate spin-torque nano oscillators (STO). These devices are aimed to be used in hard-disk drives for microwave-assisted magnetic recording (MAMR) an alternative approach to HAMR for the extension of the storage density.
Another hot topic in the magnetic community are magnetic Skyrmions. These particle-like topological structures have remarkable properties and may become a candidate for future storage technologies. We investigate the stability of these structures as well as their interaction with electric currents and spin currents.
Selected Publications
- Abert, Claas. "Micromagnetics and spintronics: models and numerical methods." The European Physical Journal B 92.6 (2019): 120.
- Palmesi, Pietro, et al. "Highly parallel demagnetization field calculation using the fast multipole method on tetrahedral meshes with continuous sources." Journal of Magnetism and Magnetic Materials 442 (2017): 409-416.
- Bruckner, Florian, et al. "Solving Large-Scale Inverse Magnetostatic Problems using the Adjoint Method." Scientific reports 7 (2017).
- Vogler, Christoph, et al. "Heat-assisted magnetic recording of bit-patterned media beyond 10 Tb/in2." Applied Physics Letters 108.10 (2016): 102406.
- Abert, Claas, et al. "A self-consistent spin-diffusion model for micromagnetics." Scientific reports 6 (2016).
- Suess, Dieter, et al. "Exchange spring media for perpendicular recording." Applied Physics Letters 87.1 (2005): 012504.
- Suess, Dieter, et al. "Time resolved micromagnetics using a preconditioned time integration method." Journal of Magnetism and Magnetic Materials 248.2 (2002): 298-311.
- Dittrich, Rok, et al. "A path method for finding energy barriers and minimum energy paths in complex micromagnetic systems." Journal of Magnetism and Magnetic Materials 250 (2002): 12-19.
